Quantas vezes você já questionou seu professor de matemática com a seguinte pergunta: “Pra que eu vou usar funções do segundo grau na minha vida?” É bem comum esse tipo de pergunta entre os alunos, porém, apesar de implícitas, as funções quadráticas e suas parábolas estão muito presentes em nosso cotidiano.
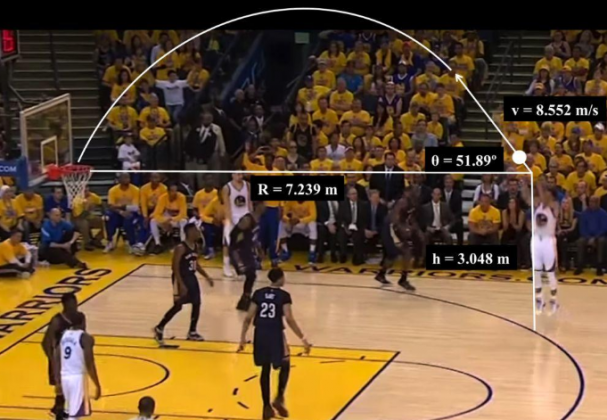
O mês de junho sempre marca o fim da temporada da principal liga de basquete do mundo, a NBA, que teve sua partida final no dia 13/06, com vitória do Toronto Raptors. Você pode estar se perguntando o porquê de estarmos falando de basquete em um texto sobre parábolas, certo?
Pois bem, se eu te disser que parábolas e basquete estão super ligados, você acreditaria?
O arremesso da imagem é um Lançamento Oblíquo, pois realiza uma trajetória parabólica nos sentidos vertical e horizontal. A bola terá sua posição inicial na mão do jogador, sendo assim, ela partirá com velocidade do seu início, depois disso, a “laranjinha” chegará em sua altura máxima e a partir daí, a bola tende a cair até chegar em sua posição final, que no caso da imagem, é a cesta.
Outro exemplo bem famoso do uso de parábolas é no famoso jogo Angry Birds (eu sei que você se viciou nesse jogo), onde utilizamos pássaros com habilidades únicas visando derrubar as bases dos inimigos, que no jogo, são representados por porcos.
Os pássaros são lançados de um estilingue, onde, começa seu lançamento oblíquo rumo à base dos porquinhos.
Logo, a matemática tem muitas aplicações cotidianas, esses exemplos retratam que os números, cálculos e funções estão diante de nossos olhos, mas, muitas das vezes, quase não os enxergamos pois estão implícitas.
Não se esqueçam das fórmulas!
Componente Horizontal(Vx) e Componente Vertical(Vy):
Vx = Vo. Cos(θ)
Vy = Vo. Sen(θ)
Alcance Horizontal:
A = V.cos(θ). t
Tempo de Subida:
t = Vy/g –> t = v.sen(θ)/g
Alcance Horizontal (Substituindo t pela equação do tempo de subida):
A = V².sen(2θ)/g
Altura Máxima:
H = Vo².sen²(θ)/2g